【理論基礎７】損失関数ー勾配降下法と最適化のしくみ

「ニューラルネットワークの多層化（MLP）」で、多層のネットワークを組めばネットワークの表現力が一気に上がる―前回そんな話をしましたが、「じゃあ、その膨大なパラメーターをいったいどう調整すればいいの？」という疑問が湧くと思います。実は、その答えとなるのが損失関数と勾配降下法という最適化の考え方です。

最初は一次関数のフィッティングからスタートして、膨大な重みを持つディープラーニングでも同じ原理でパラメーターを調整していく様子を整理します。次回以降は、この最適化がどのように可視化できるのか、さらには逆誤差伝搬法でどう計算するのかも深掘りしていく予定です。ステップを踏んで理解すれば、実はとても単純な話です。ぜひ肩の力を抜いて読み進めてみてください。

フィッティングとは？
一次関数で考えるフィッティング
ニューラルネットワークのフィッティング
1. 損失関数
2. 勾配降下法による最適化
まとめ

フィッティングとは？

「ニューラルネットワークの基本構造」で学んだように、モデルはインプットを $x$、アウトプットを $y$ として、 $y = f(x)$ という関数 $f$ で表現されます。機械学習では実用上、この関数 $f$ を「ある情報 $x$ から正解 $y$ を推論する」という解釈をします。

訓練の目的は、この関数 $f$ が「訓練データ」と呼ばれる $(x^{(i)}, y^{(i)})$ の関係を正確に再現するように調整することです。ここで i はデータの番号を表し、N 個のペアを用意します。このように、モデルをデータに「フィット」させる作業を「フィッティング」と呼びます。

一次関数で考えるフィッティング

フィッティングの簡単な例として、一次関数を考えましょう。

一次関数は次のように表されます:

$$\displaystyle y = f(x \mid a, b) = a \cdot x + b$$

ここで、$a$（傾き）と $b$（切片）がフィッティングで決まるパラメーターです。訓練データ $(x^{(i)}, y^{(i)})$ は単一の数値（スカラー）のペアで与えられます。

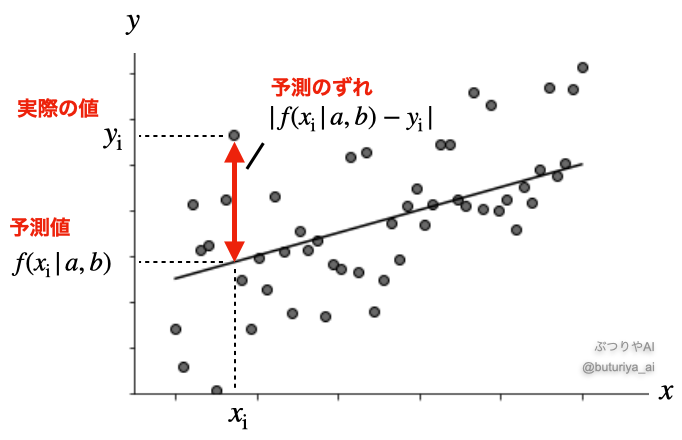
この場合、最もらしい直線を引く方法として、予測値 $f(x^{(i)} \mid a, b)$ と実際の値 $y^{(i)}$ のズレを最小化するように直線を調整します。このズレの二乗和を損失 $l$ として次のように定義します。

$$\displaystyle l = \sum_i \left(f(x_i \mid a, b) – y^{i}\right)^2$$

この損失を最小にする $a$ と $b$ を数学的に解析する方法は「最小二乗法」と呼ばれ、パラメーターは訓練データの関数として $a = a (x^{(i)}, y^{(i)})$、$b = b (x^{(i)}, y^{(i)})$と、厳密に求められます。

機械学習における一次関数フィッティングの図。データ点が散布され、最適な直線が引かれています。各データ点から直線までの距離が線で示され、この距離が損失関数（誤差）の一部として視覚化されています。数式 f(x | a, b) と予測値 y と実測値の対応関係が図示されており、最小二乗法を用いたフィッティングの概念を説明しています（出典：筆者作成）。 — 一次関数の最小二乗法によるフィッティングと損失（出典：筆者作成）

ニューラルネットワークのフィッティング

ニューラルネットワークでは、関数 $f$ の形状は設計時に決まりますが、その中の重み ${\boldsymbol W}$ やバイアス ${\boldsymbol b}$ は一次関数の $a$（傾き）や $b$（切片）に相当し、モデルの設計段階では値は未定です。ここで、ニューラルネットワークの出力 y は次のように表現されます。

$y = f(x \mid {\boldsymbol W}^{(1)}, {\boldsymbol W}^{(2)}, …, {\boldsymbol b}^{(1)}, {\boldsymbol b}^{(2)}, …)$

訓練データ $(x, y)$ は一般にそれぞれベクトル、${\boldsymbol W}^{(i)}$、${\boldsymbol b}^{(i)}$ はそれぞれ第i 層における重みの行列とバイアスのベクトルです（行列・ベクトルになることがわからない方はこちら）。従って、膨大（数万や数百万）な数のパラメータが複雑なネットワークモデルの中に散りばめられており、最小二乗法のように解析的に求めることは不可能です。では、このパラメーターは一体どのように決めればよいのでしょうか？

損失関数

ニューラルネットワークでも損失関数 $l$ を定義し、それを最小化することでパラメーターを調整します。一次関数の例では、予測値 $y = f(x^{(i)} \mid a, b)$ と実際の値 $y^{(i)}$ のズレを二乗して合計した量が損失関数でした。同様に、ニューラルネットワークでも予測値と正解のズレを基に損失関数を定義します。

損失関数はモデルのアウトプット $y$ の性質に応じて異なる形になりますが、基本的にズレの大きさを測るように定義されます。一次関数の例で使ったものは推定値と正解のズレの二乗平均なのでMSE (Mean Squared Error) と呼ばれ、ディープラーニングでもよく使われます。

勾配降下法による最適化

損失関数を最小化するために、パラメーターをどのように調整すればよいでしょうか？しらみ潰しにパラメーターを変えて損失関数を調べるのは非現実的です。例えば、たった100個のパラメーターでも、それぞれを例えばある値から $+\delta$ か $- \delta$ だけ変化させる組み合わせは $2^{100} \sim 10^{30}$ 通りとなり、それら全パターンの損失を計算しようとしても、コンピューターでも全く歯が立ちません。ここで役立つのが「勾配」の考え方です。

勾配を使う最適化は、山の中で下るのに似ています。木々に遮られて全体の地形は見えないですが、周辺の勾配（地面の傾き）を頼りに、より低い地点を目指すことで下れます。損失関数も、下の図のように、全体の形を全て調べなくても、ある地点（パラメーター）での勾配を計算することで、そこから「パラメーターをどちらの方向にどれだけ動かせば損失関数を減らせるか」がわかります。

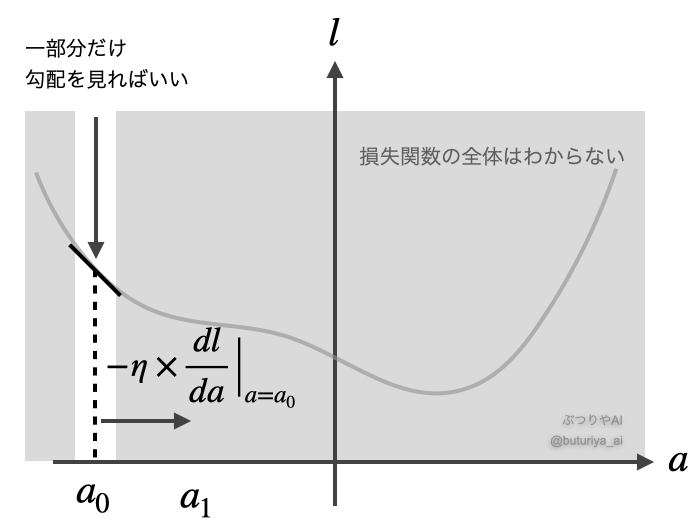
勾配降下法の概念を示す図。横軸はパラメーターa、縦軸は損失関数lを表し、損失関数全体の形は不明だが、局所的な勾配を使って損失を減らす方向にパラメーターを更新する様子が示されています。現在のパラメーターa0における勾配が矢印で強調され、勾配降下法が損失最小化のための有効な手法であることを視覚的に説明しています（出典：筆者作成）。 — 損失関数と勾配：勾配を求めることで、徐々に損失を減らすようにパラメーターを更新できる（出典：筆者作成）

たとえば、パラメーターが1つだけ（$a$）の場合を考えます。まず最初に $a$ を適当な値 $a_0$ にとります。ここで、損失関数 $l$ を $s$ について微分することで地点 $a_0$ の勾配を求めます。図を見ると、傾きが負であれば、右に動くことで損失が減ることがわかります。そこで、この傾き＝勾配を利用してパラメーターを次のように更新します。

$a_1 = a_0 – \eta \times \left(\left.\frac{d l}{d a} \right|_{a=a_0}\right)$

ここで、$\eta$（イータ）は学習率と呼ばれる調整の大きさを決めるパラメーターで、私たちが設定する値です。同様に、新しく更新した地点 $a_1$ で、もう一度勾配を求めれば、今度は

$a_2 = a_1 – \eta \times \left(\left.\frac{d l}{d a} \right|_{a=a_1;}\right)$

と、更に損失が減少する方向に変更できます。このように更新を十分に繰り返して、$a_2, a_3, …$ と求めることで、損失関数を最小化する $a = a_N$ （$N$ は十分に大きい値）を求めることができます。

まとめ

今回は関数に含まれるパラメータを調整することでデータにフィットさせる「フィッティング」を学びました。しかし関数自体が非常に複雑で膨大な数のパラメータをもつニューラルネットワークの場合、数学的に最適なパラメータを求めるのは不可能です。

そこで、損失関数を頼りに、以下のステップで山を下るように損失を減少させながらパラメータを更新できることがわかりました。

最初にモデルのパラメータを適当に決める
モデルとデータの誤差を表す損失関数を計算する
損失関数をパラメータについて微分し、勾配を求める
勾配の下る方向（微分）に定数倍だけ、パラメータを更新する
ステップ 2 から 4 を繰り返す

実際には、何百万ものパラメータが層状に配置されているため、少し工夫が必要です。特に、損失関数を各パラメーターに対して微分する「偏微分」の考え方が必要になります。

次の記事「ニューラルネットワークの最適化を視覚化する」やその次の「逆誤差伝搬法とは？勾配計算による学習の仕組み」では、この勾配計算の具体的な仕組みを掘り下げて解説します。