数学の補足１ー微分とは

微分は多くの人が高校で学んだ数学の概念ですが、実は単なる抽象的な数学の概念としてだけでなく、現実世界を理解するために人間が生み出した道具でもあります。微分の本質を理解するために、ここでは単に数学的な概念としてではなく、実社会での活用例とともに説明したいと思います。

広告と売り上げの関係
微分の定義
1. だいたいの変化率
2. 厳密な変化率
微分の具体例
1. 微分の計算
2. 微分の効用

広告と売り上げの関係

例えば、あなたが会社を経営していたり、広告・マーケティングの担当者だったとしましょう。あるいは個人で物販をしているか、不動産会社で働いているかもしれません。このとき、ウェブ広告を活用して売り上げを伸ばそうと考えているとします。そこであなたは、広告をクリックした顧客が自社のホームページに訪問し、そこで商品を購入する仕組みを作りました。

お金をかけて広告を出している以上、そのクリック数がどれくらいあるのか、そして売り上げにどれくらい影響しているのかを知りたいと思うはずです。もしクリック数が増えても売り上げが大して伸びないのであれば、広告戦略を見直す必要があるでしょう。

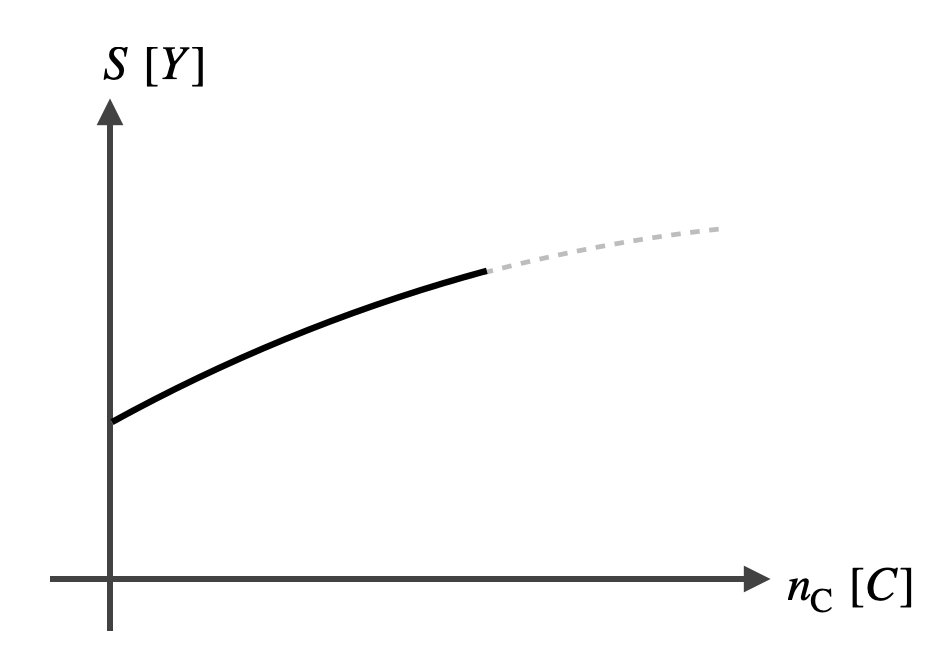
広告クリック数と売り上げが比例すると考えるのは自然ですが、実際には広告を出さなくても、すなわちクリック数がゼロでも、すでに一定の売り上げがある場合もあります（例えば常連客など）。この関係を図にすると、広告クリック数を横軸（1週間あたりのクリック数: n_C [C]）、売り上げを縦軸（週の売り上げ: S [Y; 円]）に取ったグラフで表されます。

微分の定義

だいたいの変化率

クリック数が1増えたときに売り上げが0.1円増えるのか、1万円増えるのかでは、広告の価値が大きく異なります。そこで、クリック数が1増えたら売り上げがいくら増えるのかの「変化率」を計算しましょう。例えば1週間あたりのクリック数がだいたい100に落ち着いてきたと仮定します。

図のようにクリック数がn_C = 100 [C]のとき売り上げは20万円、クリック数がn_C = 101 [C]のとき売り上げは20万1000円だとします。この場合、クリック数1あたりの売り上げの変化率は次のように求められます：

$$\displaystyle \frac{S (101) – S (100)}{101 \lbrack C\rbrack – 100 \lbrack C\rbrack}= \frac{20,1000 \lbrack Y\rbrack- 20,000 \lbrack Y\rbrack}{1 \lbrack C\rbrack} = 1000 \lbrack Y/C\rbrack$$

この計算は微分そのものではありませんが、微分の重要な考え方である「変化率」の概念を含んでいます。微分とは、2つの関連する量のうち、一方（ここではn_C）を動かすと他方（ここではS）がどれくらい変化するかを示すもので、単位が $\lbrack Y/C \rbrack$ と比率になっています（これが純粋な数学との違いで、特に物理などでは数字が意味を持つため、こういった単位が極めて重要です）。

厳密な変化率

しかし先程の計算は $n_C = 100 \lbrack C \rbrack$ と $n_C = 101 \lbrack C \rbrack$ の間の平均的な変化率です。より厳密にクリック数n_C = 100 [C]での売り上げの変化率を求めるには、例えば100 Cと100.1 Cの間での変化率を、さらに正確にするには100 Cと100.01 C …のように範囲をできるだけ狭めなければいけません。

そこで、いったん計算する区間を $\Delta n_C$ から $n_C + \Delta n_C$ までとして計算し、あとから $\Delta n_C$ を小さくする、という事を考えてみます：

$$\displaystyle \frac{\mathrm{d}S}{\mathrm{d}n_C} \Bigg|_{n_C = 100} = \lim_{\Delta n_C \to 0} \frac{S(n_C = 100 + \Delta n_C) – S(n_C = 100)}{\Delta n_C}$$

分母が無限に小さくする $\Delta n_C$ なので、式の値が無限大になってしまわないか不安に感じるかもしれませんが、図を見ればそうはならないのは明らか（傾きは無限じゃない）で、実際、Sが滑らかで普通の関数であればn_C = 100での売り上げの正確な変化率を求めることができます。これがまさに、微分の定義式になります。

微分の具体例

微分の計算

これまで売上の関数Sを考えましたが、より具体的に微分の計算例を考えてみましょう。数学の文脈では、ある関数 $f(x)$ の形が既知の場合を考えます。例えば、次のような関数を考えます：

$\displaystyle f(x) = x^2$

この関数を任意の値 $x$ の点で微分するとき、微分の定義に従って次のように計算します：

$$\displaystyle \frac{\mathrm{d}f}{\mathrm{d}x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) – f(x)}{\Delta x} $$

これに $f(x) = x^2$ を代入すると、

$\displaystyle \frac{\mathrm{d}f}{\mathrm{d}x} = \lim_{\Delta x \to 0} \frac{(x + \Delta x)^2 – x^2}{\Delta x}$

計算を進めると、

$$\displaystyle \lim_{\Delta x \to 0} \frac{x^2 + 2x\Delta x + (\Delta x)^2 – x^2}{\Delta x} = \lim_{\Delta x \to 0} (2x + \Delta x)$$

最後に $\Delta x \to 0$ とすると、

$$\displaystyle \frac{\mathrm{d}f}{\mathrm{d}x} = 2x$$

となります。

微分の効用

ところで売上Sをの右側をよく見ると、クリック数が増加するにつれて売り上げの伸びが次第に鈍化していることがわかります。これは、広告（のクリック）が増えるにつれてターゲティングが甘くなり、関心の薄い人にも表示されているためかもしれません。

クリック数を増やすには広告費がかかるため、無制限にクリック数を求めるのは現実的ではありません。そのため、例えば

$\frac{\mathrm{d}S}{\mathrm{d}n_C} = 500 \, [Y/C]$

を基準値とし、それを下回らないように広告クリック数（CPW）の目標を設定する、といった戦略を取ることができます。

ここで、広告戦略を考えるなら売上Sはクリック数の関数ではなく広告費の関数で考えるべきだと思われた方は、「数学の補足３ーチェインルール（合成微分）」を御覧ください。