【理論基礎９】誤差逆伝搬法とは？勾配計算による学習の仕組み

ニューラルネットワークはたしかに複雑なロジックを扱うことができます（ニューラルネットワークの基本要素）。しかし、それだけでは十分ではありません。ネットワークに「望む結果」を出させるためには、学習を通じてパラメーター（重みやバイアス）を適切に調整する必要があります。その調整を効率よく行う手法が誤差逆伝搬法（バックプロパゲーション）です。

誤差逆伝搬法の仕組みを理解することで、モデルの学習に関する感覚がグッと深まります。例えば、MLPの層の深さ（多さ）が学習プロセスにどう影響するかを把握しやすくなり、自分でモデルを改良する際に役立ちます。

説明上、バイアスは 0 としても本質は変わらないので、本記事では全て省略します。また、本記事では合成微分（チェインルール）を使います。馴染みのない方はあらかじめ「数学の補足３ーチェインルール（合成微分）」をご参照ください。

最新記事の更新情報等はXでお知らせしています。

目次
フォワードプロパゲーションの復習
1. フォワードプロパゲーションの流れ
2. ネットワークから損失関数へ
誤差逆伝搬法の仕組み
まとめ

フォワードプロパゲーションの復習

ニューラルネットワークは、入力データが層を通じて順次計算され、最終的に出力が得られる仕組みになっています。この入力から出力への流れをフォワードプロパゲーション（順伝播）と呼びます。

パラメーター（今回は重みのみ）は学習の一番最初のステップでは全てランダムな値を割り当てられ、その後は更新された値になります。したがって、パラメーターは学習プロセス全体を通して、常に具体的な値を持っています（ピンとこない方は損失関数ー勾配降下法と最適化のしくみから読み直してください）。

フォワードプロパゲーションの流れ

データは次のように伝搬します：

入力層: 入力データ $x^{(i)}_{j}$ を受け取る（i は訓練データの番号、j は次元）。
隠れ層: 入力データに重み $w$ をかけて変換し、活性化関数を通して次の層に渡す（ニューラルネットワークの基本要素）。

例えば、最初の隠れ層では次のように計算されます：

$$\displaystyle z^{(1)}_{i} = \phi\left(\sum_{j} w^{(0)}_{ij} \cdot x_{j}\right)$$

出力層: 最終的な予測値 $y$ を計算する。

この順伝播の計算が終わると、全てのニューロン（ノード）に具体的な数値が割り当てられます。

ネットワークから損失関数へ

順伝播でモデルが出力した値 $y_{j}$ と正解データ $y^{(i)}_{j}$ の誤差を測るために、損失関数を用います。例えば、損失関数に平均二乗誤差（MSE）を使用する場合、以下のように表されます：

$$\displaystyle l = \sum_{i,j} \left( y^{(i)}_{j} – y_{j} \right)^2$$

下のMLPの模式図のように、出力層は損失関数につながっています。フォワードプロパゲーションでは、入力から順番に値を計算して、最終的に損失関数に到達します。

誤差逆伝搬法は、この損失関数を最小化するために、全てのパラメーター（重み $w$）を調整する仕組みです。具体的には、損失関数ー勾配降下法と最適化のしくみで述べたように、「各パラメーターを少し増減」させたときに「損失がどう増減するか」＝「勾配」を調べます。

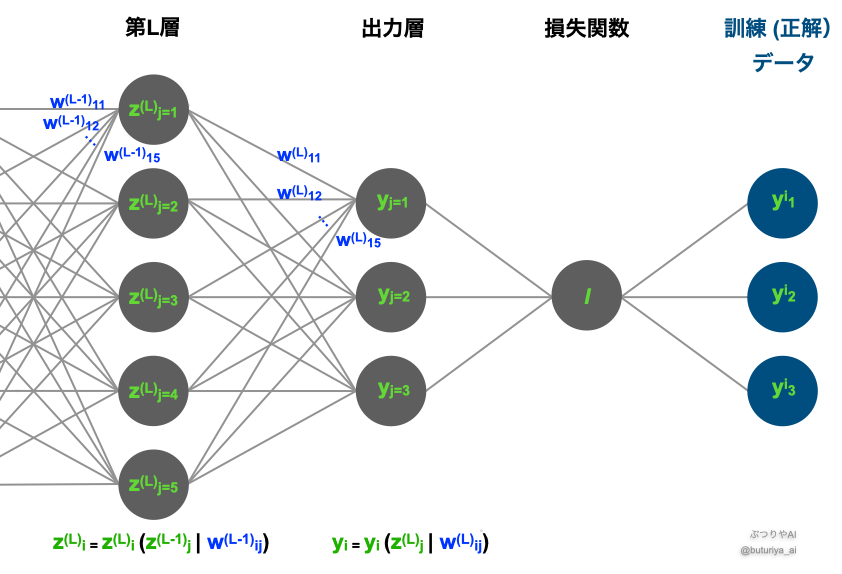
ニューラルネットワークにおける順伝播（Forward Propagation）の流れ（出典：筆者作成） — フォワードプロパゲーション模式図：各ノードの値は緑、重みは青、各レイヤーの出力値はz。zは出力をとおして重みパラメーターとを含む（出典：筆者作成）。

誤差逆伝搬法の仕組み

誤差逆伝搬法は、以下の3つのステップで構成されています：

損失関数の計算: 順伝播で得た出力層の値を使用。
損失関数の勾配（偏微分）の計算: 各パラメーターが損失関数に与える影響（勾配）を計算。
パラメーターの更新: 勾配を基に重みを調整。

これらは前の記事「ニューラルネットワークの最適化を視覚化する」ですでに説明した通りです。では前回と何が違うのかというと、ステップ２で深い層（２レイヤー以上）に一般化されている点です。

出力層での勾配計算

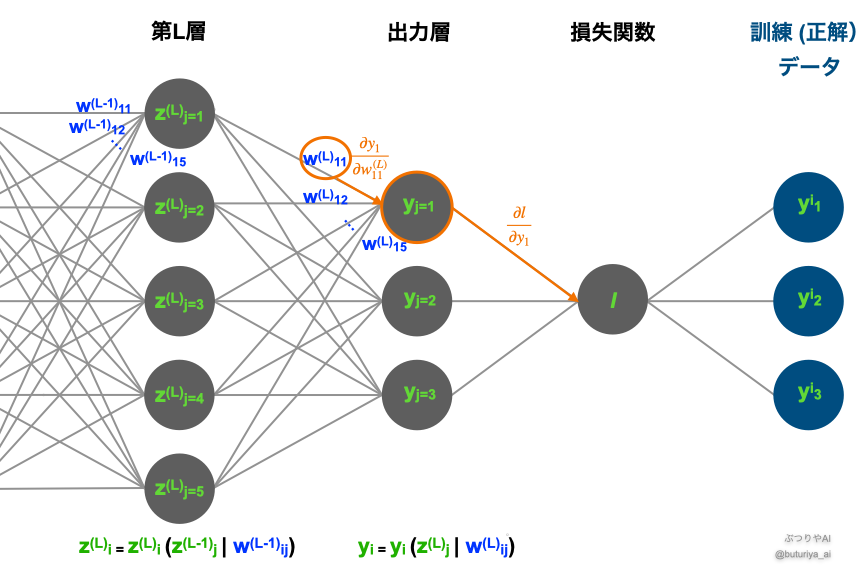
幸いなことに、出力層のパラメーター $w^{(L)}$ については、前回と全く同じです。復習も兼ねて、より具体的に損失関数の勾配を計算してみましょう：

$$\displaystyle \frac{\partial l}{\partial w^{(L)}_{ij}} = \frac{\partial l}{\partial y_{i}} \cdot \frac{\partial y_{i}}{\partial w^{(L)}_{ij}}$$

この式では、チェインルール（わからない方はこちら）を用いて勾配を2つの部分に分解できます：

$\frac{\partial l}{\partial y_{j}}$: 出力の変化が損失に与える影響の大きさ。
$\frac{\partial y_{i}}{\partial w^{(L)}_{ij}}$: 重みの変化が出力に与える影響の大きさ。

これらは下図のオレンジの矢印に対応し、 $w^{(L)}$ から損失 $l$まで、隣あうもの同士の微分（勾配）をかけていることがわかります。

ディープラーニングの逆誤差伝搬模式図。損失関数から出力層の活性化関数に誤差が伝搬する経路をハイラ>イトした図。数式付きで誤差がどのように損失関数に伝搬するかを示しています（出典：筆者作成）。 — 誤差逆伝搬法における出力層から損失関数への誤差伝搬の経路。

隠れ層での勾配計算

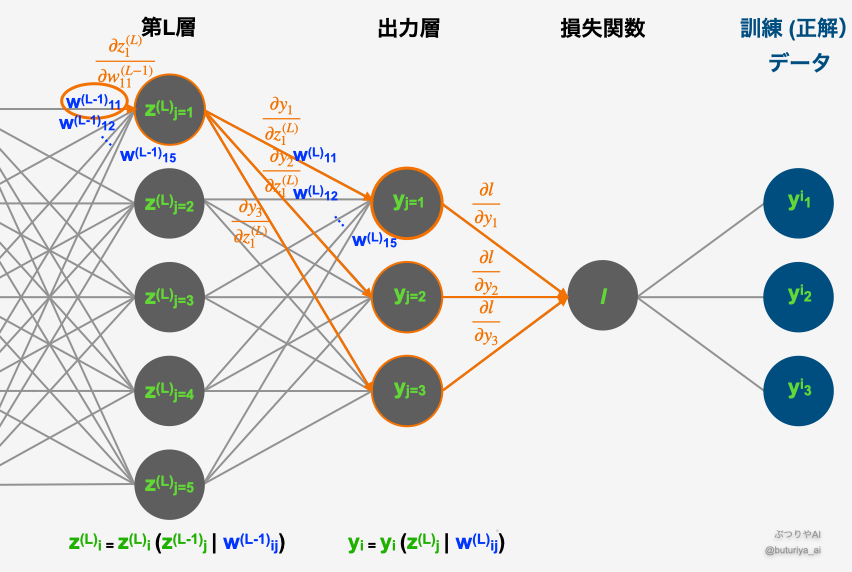
次に、隠れ層における勾配を計算しましょう。ここでもチェインルールを用い、隠れ層の重み $w^{(L-1)}$ に関する勾配を求めます：

$$\displaystyle \frac{\partial l}{\partial w^{(L-1)}_{ij}} = \sum_{k} \left( \frac{\partial l}{\partial y_{k}} \cdot \frac{\partial y_{k}}{\partial z^{(L)}_{i}} \cdot \frac{\partial z^{(L)}_{i}}{\partial w^{(L-1)}_{ij}} \right)$$

ここでは、パラメーター $w^{(L-1)}$ の変化が出力層を通じてどのように損失に影響を与えるかを計算しており、勾配は次の３つに分解されます：

$\frac{\partial l}{\partial y_{k}}$: 出力の変化が損失に与える影響の大きさ。
$\frac{\partial y_{k}}{\partial z^{(L)}_{i}}$: 隠れ層のニューロンが次の出力層に与える影響の大きさ。
$\frac{\partial z^{(L)}_{i}}{\partial w^{(L-1)}_{ij}}$: 重みの変化が隠れ層のニューロンに与える影響の大きさ。

これらは下図のオレンジの矢印に対応し、$w^{(L-1)}$と $l$ を結ぶ全ての経路に関して、隣あう微分（勾配）を掛けた後に足し合わせていることがわかると思います。

もう一つ重要な点として、ステップ１の値は上の「出力層での勾配計算」ですでに求められているため、そのまま再利用ができます。さらに浅い層の重み$（w^{(L-2)}, w^{(L-3)}, …$）に関する勾配を計算するときにも同様で、１ステップ目の計算はそれよりも前の計算結果を使いまわせます。

ディープラーニングの逆誤差伝搬模式図。出力層の活性化関数から損失関数に誤差を伝搬する経路をハイラ>イトした図。数式付きで誤差が層（レイヤー）をまたいでどのような経路で損失関数に伝搬するかを示しています（出典：筆者作成）。 — 逆誤差伝搬法における出力層から損失関数への誤差伝搬の経路（２）

パラメーターの更新

勾配が計算できたら、次はパラメーターの更新を行います。更新は以下の式に基づいて進められます：

$$\displaystyle w_{ij} \leftarrow w_{ij} – \eta \frac{\partial l}{\partial w_{ij}}$$

ここで、η は学習率です。このように、「損失計算」、「勾配計算」、「パラメーターの更新」を繰り返すことで、損失関数の値を徐々に小さくし、モデルの精度を向上させていきます。

まとめ

フォワードプロパゲーションでは、入力データが層を通じて変換され、最終的な出力が得られます。この出力と正解データの誤差を測るために損失関数を使用し、学習の指標とします。

誤差逆伝搬法では、損失関数の値を小さくするために、各層のパラメータ（重み）に対する勾配を計算し、それに基づいてパラメータを更新します。この勾配計算にはチェインルールを用い、層を遡る形で誤差を伝搬させます。

この一連のプロセスを繰り返すことで、ニューラルネットワークは徐々に最適な重みを獲得し、より正確な予測ができるようになります。

ディープラーニング入門【初心者向け】の「理論基礎編」は以上になります。以下、続きの３つの記事はこれまでに使った数学の補足となります。

より実践的な内容を学びたい方は、引き続き「実践基礎編」へお進みください。