【理論基礎８】ニューラルネットワークの最適化を視覚化する

損失関数の最適化はシンプルな1次元のパラメーターでも説明できます（損失関数ー勾配降下法と最適化のしくみ）。しかし、ニューラルネットワークの最適化では、膨大な次元のパラメーター空間を扱う必要があります。ここでは、パラメーターが２次元（重み $w$ とバイアス $b$）の場合で損失関数を視覚化しながら、パラメーター更新がどのように進むかをより立体的に捉えましょう。前回の１次元の例に比べ、２次元はより高次元のイメージにかなり近くなるため、非常に重要です。

損失関数の視覚化
偏微分を用いた勾配の計算
1. 重み $w$ に関する偏微分
2. バイアス $b$ に関する偏微分
等高線と更新の軌跡
まとめ

損失関数の視覚化

非常に単純なモデルとして、隠れ層のない入力層と出力層から成るニューラルネットワークを考えます。この場合、モデルは次の形式になります：

$\displaystyle y = f(x \mid w, b) = \varphi(w \cdot x + b)$

式が少し回りくどいようですが、出力層の値 $y$ は関数 $f$ で、$f$ の具体的な形は活性化関数 $\varphi$、という意味合いです。訓練データ $(x^{(i)}, y^{(i)})$ にモデルをフィッティングするために、損失関数を定義します。前回と同様、損失関数 $l$ は平均二乗誤差 (MSE)を使います：

$$\displaystyle l = \sum_{i} \left( y^{i}- y^{(i)} \right)^2$$

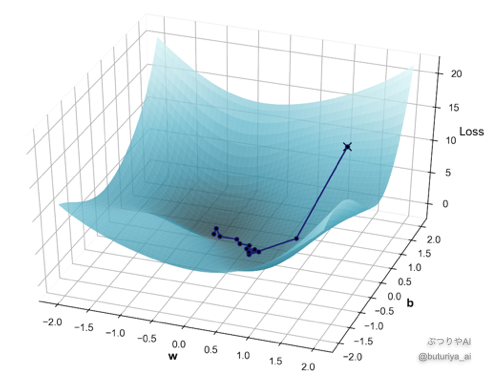
ここで $y^{i}$ は入力 $x^{(i)}$ に対するモデルの出力です。この損失関数は、重み $w$ とバイアス $b$ の空間上で定義されますが、その形状はモデルとデータに依存し、通常、私たちには分かりません。しかし仮にあらゆる $w$, $b$ の値で損失関数を計算し、その形状を視覚化したら、だいたい図のようになっていると思われます。どこかに谷底が存在し、その底に対応する $(w, b)$ が損失関数を最小にする、求めたいパラメーターの値となります。

2つのパラメーター（重み w とバイアス b）を用いたニューラルネットワークの損失関数の3D視覚化。損失関数の谷底に向かうパラメーター更新の経路を勾配法（勾配降下法）で示しています

偏微分を用いた勾配の計算

実際には損失関数の全貌はわからないため、まずは最初のとっかかりとして最初に適当な初期値 $(w_{0}, b_{0})$ を決め、その地点での損失関数を計算します。図の中ではこの位置をバツ印で表しています。次に、この点から損失関数を減少させる方向を計算し、パラメーターを更新します。この減少方向を求めるために、今回は偏微分（わからない方はこちら）を用います。

重み $w$ に関する偏微分

偏微分とは、着目する変数以外を定数だと思って、着目する１変数についてのみ微分することです。ここでは $b$ を無視して、$w$ について微分することになります。合成関数の微分を使って計算すると、以下のようになります。

$\displaystyle \frac{\partial l}{\partial w} = \sum_{i} \frac{\partial l}{\partial y}\Big|_{y = y^{i}} \frac{\partial y}{\partial w}\Big|_{x = x^{(i)}}$

ここで、$x^{(i)}$は入力した訓練データ、$y^{i}$は$x^{(i)}$ を入力したときのモデルの出力で、第二項の中の $w$ と $b$ には暫定的に決めた$w_0$、$b_0$ を代入します。

バイアス $b$ に関する偏微分

今度は $w$ を固定して、$b$ について微分します。

$\displaystyle \frac{\partial l}{\partial b} = \sum_{i} \frac{\partial l}{\partial y}\Big|_{y = y^{i}} \frac{\partial y}{\partial b}\Big|_{x = x^{(i)}}$

これら $(w_0, b_0)$ における勾配の方向へ、パラメーターを次のように変更します：

$$\displaystyle w_1 = w_0 – \eta \times \frac{\partial l}{\partial w}\Big|_{w=w_0, b=b_0}$$

$$\displaystyle b_1 = b_0 – \eta \times \frac{\partial l}{\partial b}\Big|_{w=w_0, b=b_0}$$

ここで学習率 $\eta$（イータ）は更新の大きさを表しており、私たちが予め決めておく値です。

等高線と更新の軌跡

先ほど、$w = w_0$、$b = b_0$ における勾配を求め、それに学習率 $\eta$ の分だけ変更しました。これは、新しいパラメータ $w = w_1$、$b = b_1$ でもくりかせます。このプロセスを何度も繰り返すことで、損失関数が最小になる谷底に向かってパラメーターが少しずつ近づいていきます。最初の図に示した軌跡が、この様子を表しています。

しつこいようですが、学習過程で、あくまで私たちはパラメーター空間全体での損失関数の値は知らず、軌跡上の各点での勾配しか求めていないことに気をつけてください。パラメーターが２つならなんとか全て計算できそうですが、何百万パラメーターの空間上全ての点での損失関数の計算は不可能なため、こういった戦略をとるのです（パラメータ空間の広さについては「脳は宇宙よりも広い？〜ニューラルネットワークの広大な世界」）。

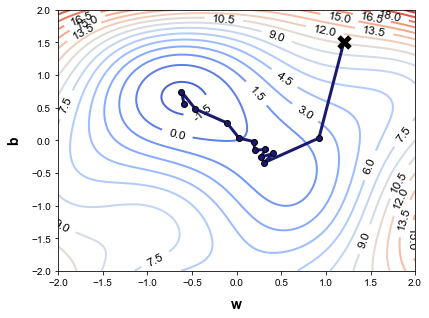
以下の図は、学習ステップごとのパラメーターの軌跡を損失関数の等高線と一緒に示しています。各点が次の点に向かう方向は、等高線に直交していることがわかります。これは、偏微分が損失関数を最も急激に減少させる方向を示しているためです。

このように、ニューラルネットワークでは、複雑な多次元パラメーター空間における損失関数の勾配を利用しながら、繰り返しパラメーターを更新して最適化を行います。

実際には何万、何百万の重みやバイアスを扱うので、今回のように２次元平面でパラメーターの軌跡を図示することは不可能で、はるかに高次元の空間の中を、複雑な軌跡を描いて移動していきます。

ところで冒頭に、２次元は１次元よりも高次元のイメージに近い、と言いました。これは、２次元になると小さな丘があったり、その丘を避けるような回り道があるためです。こういったイメージを膨らませておくと、ディープラーニングを使うときに、より親近感を覚えるかもしれません。

ニューラルネットワークにおける2つのパラメーター（重み w とバイアス b）の損失関数の等高線図。初期値から勾配降下法を用いて損失を最小化する経路を示したトップビュー。 — 損失関数の等高線と更新パラメーターの経路

まとめ

入力が１個、ニューロンが１個でパラメータが重み $w$ とバイアス $b$ の場合で、損失関数を視覚化しました。パラメータが２つの場合、パラメータ空間に損失関数を表示すると山や谷が現れることがわかりました。モデルの最適化は谷底でのパラメータの値を見つけることに対応します。実際には同じようなことがより高次元のパラメータ空間で行われます。