基本的なニューラルネットワークである MLP (Multi-Layer Perceptron) がなぜ画像に適さないかを明確にし、それと対比しながら CNN を説明します。最後に、CNN に置ける特徴マップやカーネルを単位とするとCNN は実は MLP と同じ構造を持っていることを示します。
最新記事の更新情報等はXでお知らせしています。
FCNの問題点

(1)爆発的に増えるパラメータ
一般的な画像のサイズを考えると、例えば 256 × 256 ピクセル(約 6 万ピクセル)、512 × 512 ピクセル(約 26 万ピクセル) など、入力の次元数は非常に大きくなります。
仮に FCN で 512 × 512 ピクセルの画像を処理するとしましょう。入力層が 26 万ノード、中間層も 26 万ノード だとすると、重みのパラメータだけで 26万 × 26万 ~ 680 億個 になります。さらにもう一層追加すると、パラメータの数は 10¹⁶ 個以上 になり、計算コストが爆発的に増加します。
(2)位置情報の喪失
FCN では、画像のピクセルを単純に 1 次元のベクトル として扱うため、空間的な関係が失われます。たとえばあるピクセルがどのピクセルと隣接しているのか(上下左右、斜めの関係)が分からなくなります。そのため、エッジやテクスチャ、形状などの局所的な特徴を捉えるのが困難になります(原理的には FCN でも学習可能ですが、自由度が高すぎて現実的ではありません)。
(3)平行移動やスケール変化に弱い
FCNでは、入力画像のピクセルごとに独立した重みを学習するため、物体の位置が少しズレるだけで異なる入力として認識されてしまいます。例えば、犬の画像が中央にある場合と右下にズレた場合では、FCN にとっては全く異なるデータとして扱われるため、汎化性能が低下します。
CNNの構成要素
CNN は FCN の無駄な自由度を削減し、画像の空間構造を保持したまま処理できるように設計されており、基本構造は以下の要素から成ります。
- Convolution Layer(畳み込み層)
- 活性化関数(ReLU など)
- Pooling Layer(プーリング層)
畳み込み層(Convolution Layer)
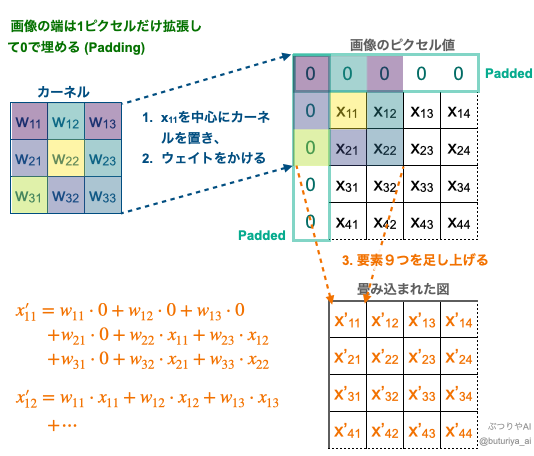
畳み込み層は、画像から局所的な特徴を抽出するために用いられます。FCN の全結合層における重み付き和と同様に、畳み込み層でも重みを適用して特徴を抽出します。そのため、原理的には FCN の重み構造に大幅に制限をかけたものと同じです。手順は以下のとおりです。
- カーネル(重み)を画像のあるピクセル位置に重ねる。
- カーネルの重み ( \(w_{i, j}\) ) と重なったピクセル値 ( \(x_{i, j}\) ) を掛け算する。
- すべての積を合計して出力値を得る。
- カーネルをスライドさせて全ピクセルに対して繰り返す。
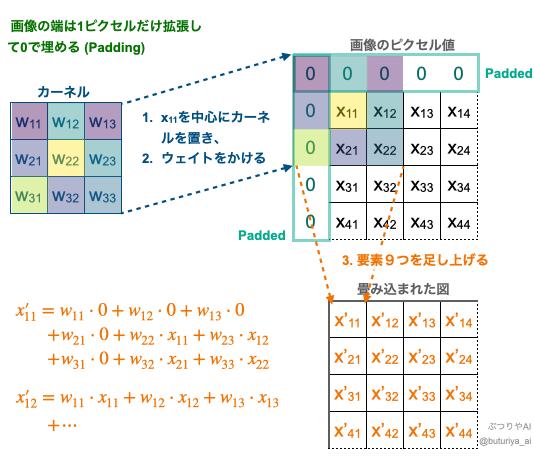
Covolution layer における畳み込み(出典:筆者作成)
さらに ReLU などの活性化関数を適用したものを特徴マップ(Feature Map)といい、特徴マップ毎に様々な特徴を捉えることができます。上の図では、畳み込まれた図が元の図と同じマトリックスサイズになるように、畳み込む前の図の外側に1ピクセル分だけ0という値を付け加えています(0 Padding)。
畳み込みには、次の2つのメリットがあります。
局所的な特徴量の抽出
特徴マップの各ピクセル(\(x’_{11}\)など)は、その前の層の同じ位置のピクセルとその周辺だけを見ることになります。これにより、エッジやテクスチャなど、局所的な特徴量を抽出することができます。探し出したい特徴(例えばネコの耳など)がどこにあっても、異なる位置で同じ特徴量が得られます。
パラメータの節約
一般的にカーネルは 3 × 3 か、大きくても 7 × 7 程度であり、FCN に比べてかなりパラメータの数が少なくなります。更に、1つの特徴マップを作るのに1つだけのカーネルを使っています(例えば、\(x’_{11}\)、\(x’_{12}\) どちらの計算にも、同じカーネルを使いまわします:参考)。これによって、使用するパラメータの数が大幅に削減されます。
プーリング層(Pooling Layer)
プーリング層は、以下の手順で特徴マップのサイズを縮小し、計算量を削減することができます。
- 特徴マップを 2 × 2 の小領域に分割。
- 各領域の最大値(Max Pooling)または平均値(Average Pooling)を取得。
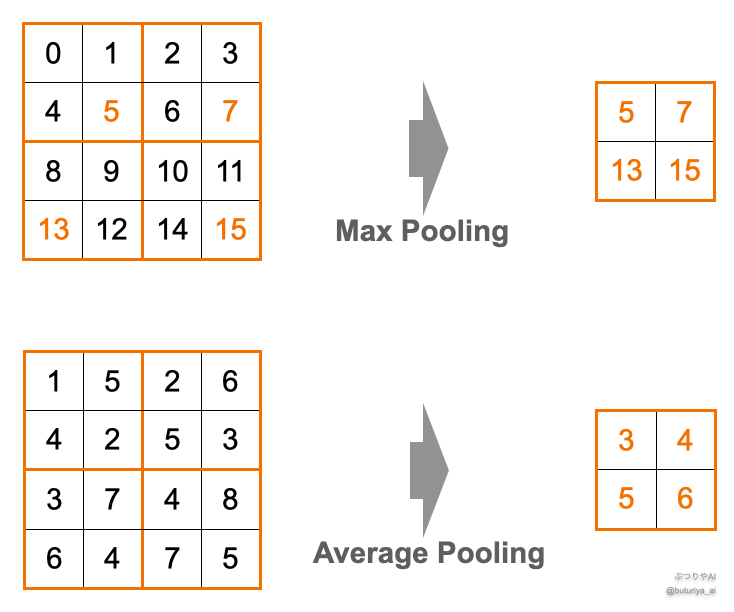
出典:筆者作成
プーリング層のメリットは以下のとおりです。
冗長な情報と計算コストの削減
Pooling Layer を通すことで特徴マップのサイズが小さくなります。あとに続く層で、畳み込みの計算をするピクセル数が減ります。特に Max Pooling を使うことで、それぞれの小さい領域 (2 × 2) で最も大きな特徴量だけを残すので、あまり重要ではない冗長な情報を減らすことができます。
大域的な特徴の抽出
畳み込みは局所的な特徴を抽出するのに優れていますが、逆に大域的な特徴を抽出するのが難しくなります。Pooling Layer はそのような弱みを補うことができます。Pooling Layer を通って画素を荒くすることで、適度に大域的な特徴を抽出できるようになります。
平行移動に対する安定性
例えば Max Pooling の処理を一回すると、入力の特徴マップの中で捉えたある特徴(例えば犬の耳など)の場所が1ピクセルズレても基本的に同じ結果が得られます。図中で言えば、5 という値が左に1ピクセルズレても Max Pooling の出力は同じになりますよね。そのため、物体の位置に対して出力が安定します。
CNNの構造
特徴マップの多チャネル化
実は”画像”、あるいは”特徴マップ”を1つの単位としてみると、CNN で構成されるモデルは FCN と全く同じ構造を持っています。以下の図は、MNIST と呼ばれる手書き数字の画像を 0 ~ 9 に分類するように訓練した時の実際の特徴マップです。特徴マップはレイヤーごとに複数使用し、並べる次元をチャネル (channel) といいます。入力データも channel の次元を持っており、カラー画像であれば RGB で 3 チャネルのデータになります。入力層から最初のレイヤー (Conv + ReLU) につながる線毎に 3 × 3 の「カーネル = 重み」とバイアス 1 つ、合計 10 個のパラメータが割り当てられます。
最初の特徴マップは 2 × 2 ピクセルごとに Max Pooling で最大値のみ抽出され、また次のレイヤーと繋がります。例えば図中の Conv + ReLU の特徴マップのチャネルがどちらも 64 であれば、パラメータの数は、重みが 64 × 64 × 9 = 36864 個、バイアスはつながる先のノード毎に足されるので 64 個で、計 36928 個となります。
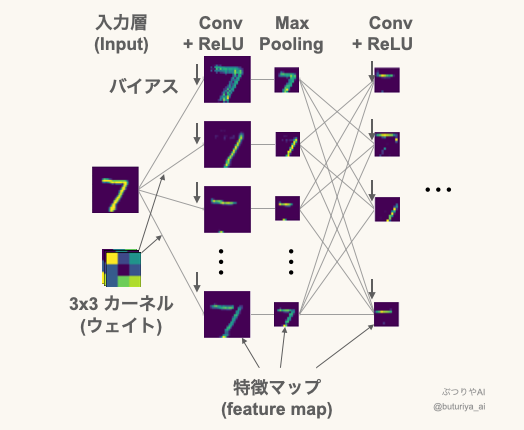
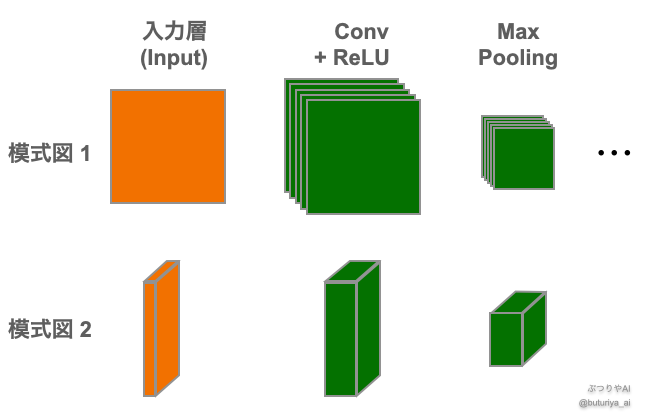
代表的な CNN の模式図:特徴マップの表現方法(平面 vs. 立体)
先程の図は特徴マップを1つの単位とすると FCN と同じ構造になることを図示したものですが、一般的には下の図のように表されます。図上部では特徴マップは正方形で表され、重ねる量で定性的に特徴マップの数を表現します (参考:DenseNet)。Pooling Layer を通って特徴マップが小さくなると、正方形も小さくなります。立方体の場合は特徴マップの大きさは高さと奥行きで表現され、特徴マップの数が多くなるほど幅が厚くなります (参考:VGGNet)。
まとめ
CNN は FCN の自由度を適切に制限することでパラメータ数を削減し、空間構造を捉え、位置のズレやスケール変化に対してロバスト(頑強)な結果を得ることができます。畳み込みを行う 3 × 3 や 5 × 5 ほどのカーネルが重みパラメータとなり、学習を通してどのような特徴を抽出すべきかを学びます。畳み込みのあとに活性化関数に通したものを特徴マップといいます。
入力層から出力層まで、データはチャネル (channel) の次元を持ち、中間層ではチャネルの数の分だけ特徴マップが作られます。特徴マップを1つの単位とすると、CNNはFCN と同じ構造を持ちます。
畳み込みについてはGoogle の資料にも視覚的でわかりやすい説明があります。以下の動画は視覚的かつ直感的にわかります。
コメント