ディープラーニングで Numpy ではなく Tensor が使われる大きな理由の一つが「自動微分」です。学習の際には、何百万、何千万パラメータについてチェインルールに基づいて微分を行う必要があり、自動微分は必須となります。これは、さらに Tensor の機能で GPU を利用することで大きな威力を発揮します。
<概要>
- Tensor の backward() による自動微分の計算方法
- optimizer.step() による誤差逆伝播法
を中心に、実際のコードとその挙動を、グラフや図を交えながらビジュアルに説明します。
<この記事で扱う主要なモジュール・ライブラリ一覧>
import torch<関連記事>
- ディープラーニング入門【初心者編】
- 【実践基礎6】PyTorchのDatasetとDataLoaderを理解しよう
- 【実践基礎7】PyTorchのTensorを理解しよう
- 【実践基礎9】PyTorchモデルの全体構造と作り方を理解しよう
<コード>
計算グラフ
Tensor では、複雑な関数に含まれる大量のパラメータについて自動微分を行うために、計算グラフを使います。グラフは普段は隠れて見えず、特に意識しないでいいですが、Tensor のイメージを掴むために、1次関数の計算グラフを簡単に眺めてみましょう。
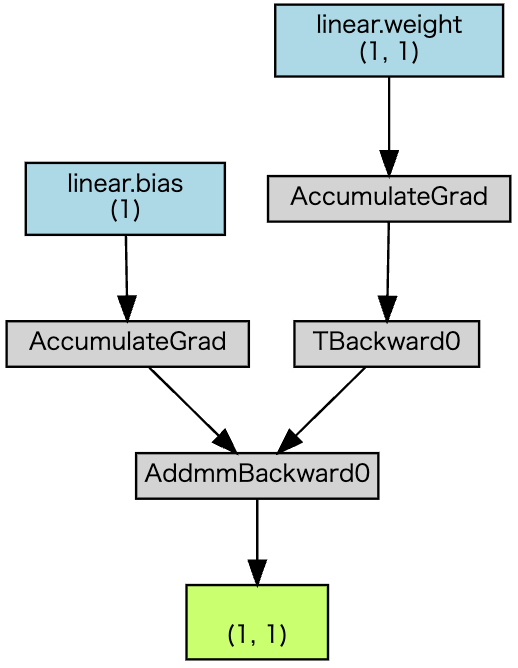
水色の ”linear.bias” が切片、”linear.weight“ が傾き、そして緑の箱が出力です。データのサンプル数の次元があるため、データの形がスカラーではなく (1, 1) となっています。矢印を遡って出力(緑)からパラメータ(青)までたどることで、チェインルールに則って偏微分を行う経路がわかります。
グラフ中の “AccumulateGrad” は、自動微分を行うたびに、モデル(関数)の各パラメータに関する偏微分の値が加算されながら、その値が保持されることを表しています。ミニバッチ学習などでは、ある程度まとまったデータ毎に勾配を平均してから誤差逆伝播をするため、値が加算されるのは理にかなっています。
※ モデルを正しく作れているかを視覚的に確認するのに torchviz は便利ですが、ディープラーニングの学習には特に必要ありません。
Tensorの自動微分
rquires_grad
ある Tensor を使って関数を作るときに、Tensor を requires_grad=True とすることで、関数を微分するときの変数として扱われます。教師あり学習で使われる損失関数は、「入力データ」、「重みやバイアスなどモデルのパラメータ」、そして「正解データ」を Tensor として持っています。入力データと正解データは変えることのできない所与の値であり「定数」ですが、調整すべきモデルのパラメータは「変数」なのでrequires_grad=Trueと設定します。
# パラメータ "w" を、勾配を求めるときに変数として扱うことを宣言
import torch
w = torch.tensor([1.0], requires_grad=True)PyTorch の torch.nn.Module を用いてモデルを構築する場合、パラメータは自動的に requires_grad になるため、普通の学習では requires_grad を気にする必要はありません。しかし、遷移学習 (Transfer learning) やニューラルネットワークモデルを損失関数の計算に使う perceptual loss などでは、パラメータ(の一部)を固定するため、requires_grad = False として勾配計算をオフにするなど、細かい設定が必要となります。
loss.backward()
Tensor 変数 loss についての微分を計算します。値は 各 Tensor 変数 (パラメータ) の grad という属性に格納されます。属性とは numpy であれば .shape がそれに当たります。たとえばあるパラメータ w の微分値は w.grad となります。.backward() で微分を計算すると、毎回新しい微分値に更新されるのではなく、現在の .grad の値に加算されていきます。
loss.backward()ここで loss は単に Tensor からなる関数であり、backward() は任意の Tensor からなる関数でできる操作であることに注意してください。
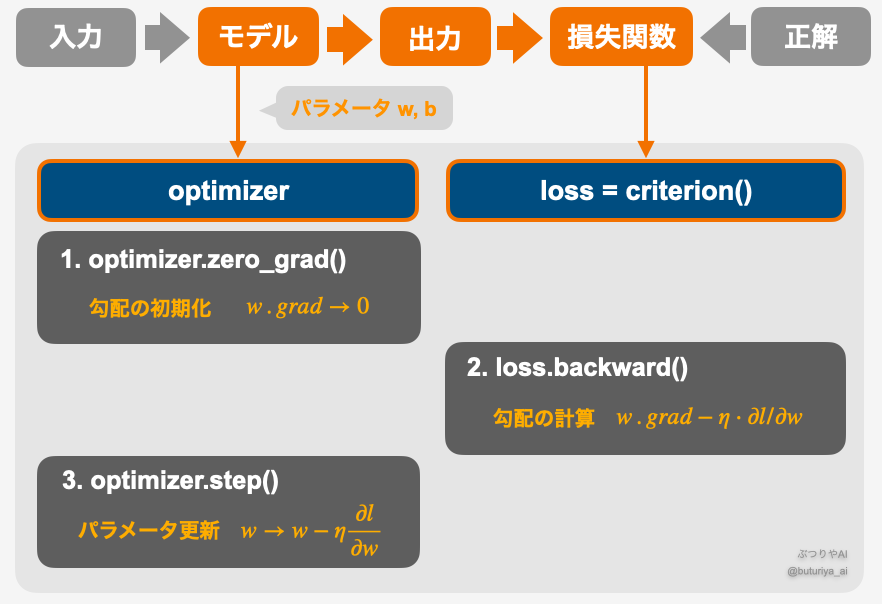
optimizerで誤差逆伝播
Optimizerの設定
.backward() を使えば、損失関数をすべてのモデルパラメータについて一行で微分できることがわかりました。次に、勾配をもとにすべてのパラメータを更新する必要があります。まずは以下のように、最適化アルゴリズムを指定して optimizer オブジェクトを作ります 。
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # SGDで最適化
optimizer = torch.optim.Adam([var1, var2], lr=0.001) # Adamで最適化optimizer の最初の引数は全パラメータを含んだ iterable (イテラブル; リストなどのように、for loop で値を取り出せる)です。ここで学習率なども必要に応じて指定します (公式リンク)。
optimizer.step()でパラメータ更新
Optimizer オブジェクト optimizer には step() メソッドがあります。step() は、先程のloss.backward() で求めた 勾配の値 (.grad) を使ってパラメータを更新します。
optimizer.step()optimizer.zero_grad()
パラメータの grad 属性にある勾配を初期化します。backward() で説明したように、微分値は計算されるたびに加算されていくので、例えばミニバッチ毎に学習する場合、バッチ毎に最初にzero_grad による初期化が必要です。
optimizer.zero_grad()コードで実践
一般的な学習の仕組みと手順は以下の通り、1. zero_grad() でパラメータを初期化、2. backward() で勾配計算、 3. step() でパラメータを更新、となります。オレンジ色 (モデルから損失関数、optimizer 、 loss) は計算グラフ上、すべて Tensor 型のパラメータ w、b で繋がっています。
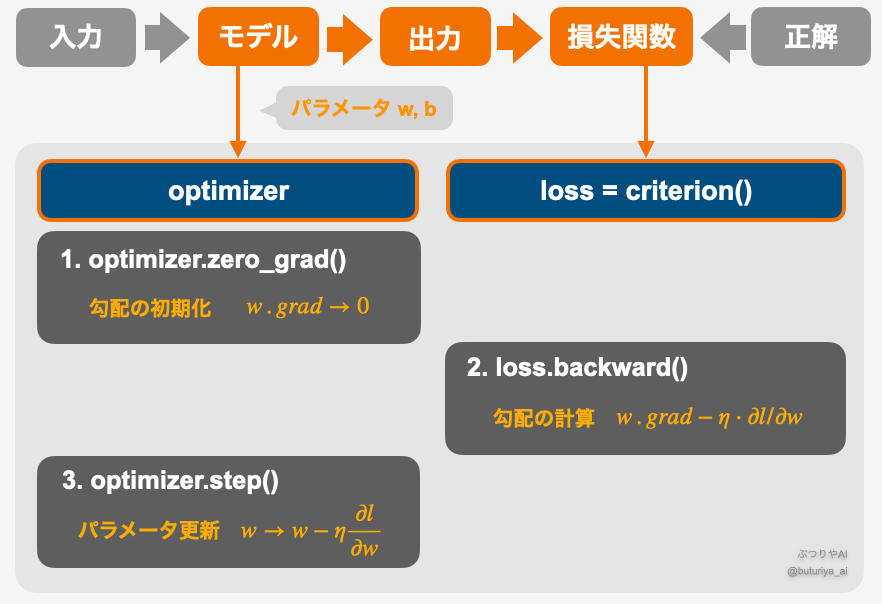
より具体的に Tensor による微分を理解するために、上の手順に沿って、手作りの 1 次関数で学習の様子を見てみましょう。といっても肝心の部分は 10 行ほどです。Tensor の具体的な挙動の理解は、単にイメージを掴むためだけでなく、遷移学習など、後々の応用でも必要になってきます。
Tensorでデータとモデルの準備 (requires_grad, zero_grad)
まずは訓練用の入力データ (x_train)、正解データ (y_train)、そして傾き w = 1 の一次関数モデルを Tensor で準備します。
import torch
# 訓練データ
x_train = torch.tensor([0, 1, 2, 3]) # 入力(テンソル)データ
y_train = torch.tensor([0, 2, 3, 3]) # 正解(テンソル)データ
# 傾きwの1次関数のモデル
def net(x, w):
return w * x
# パラメータの初期設定 (テンソル w)。勾配を計算したいので requires_grad=True を設定
w = torch.tensor([1.0], requires_grad=True)
# 最適化アルゴリズム
optimizer = torch.optim.SGD([w], lr=0.01) # パラメータ w を iterable (list) :[w] として optimizer にわたす
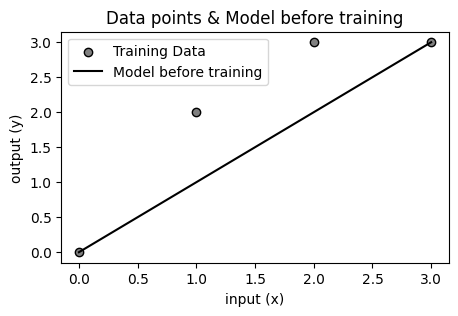
optimizer.zero_grad() # パラメータの勾配を初期化訓練では最初、パラメータにランダムな値が振られます。今回はその値がたまたま 1 としました。下のプロットを見ると、データ点がモデルよりやや上に分布しているので、理想的な傾きは 1 よりやや大きいことがわかります。
最適化アルゴリズムとして、挙動がわかりやすい SGD を学習率 lr = 0.01 で使用しています。今回は初期化は特に必要ないですが、ループを回すときなどは zero_grad() を最初に書く必要があります。
Tensorで誤差逆伝播 (loss.backward, optimizer.step)
以下、順伝播、損失の計算、勾配計算からパラメータの更新までのコードです。
# 順伝播
y_pred = net(x_train, w)
# 損失関数
loss = torch.sum((y_pred - y_train)**2)
# 勾配計算 (requires_grad で変数とみなされた w についてのみ勾配を計算)
loss.backward()
# 勾配の確認
print(f"w.grad: {w.grad}") # 全データについて勾配が足し合わされ、grad属性に値が入る
optimizer.step() # パラメータの更新
print(f"w: {w}") # 先ほど求めた勾配 x (-1) x lr になるloss.backward() の際、損失関数 loss には3種類の Tensor (x_train, y_train, w) が含まれていますが、requires_grad = True としたパラメータ w のみが変数とみなされ、loss を w について偏微分した値 w.grad のみが計算されます。
勾配の値 w.grad は今回は “-6” となります。optimizer.step() では、新しいパラメータは
$$\displaystyle w→w−\eta\frac{∂l}{∂w}=w−lr×w.grad$$
となるため、更新したパラメータの値は 1.06 と表示されます (最適化の基礎と勾配降下法についてはこちら)。
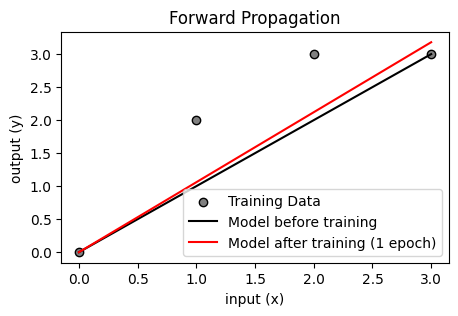
誤差逆伝播の結果
今回はデータセットが1セット (x_train, y_train) ですべてなので、これで 1 エポック分の学習が終わったことになります。上で学習したモデルをプロットすると、傾きがやや増加して、データ点に近づいていることがわかります。大量のデータでミニバッチ学習をする場合は、このデータ点はバッチごとに変わり、データに合わせて傾きが少しずつ変化していきます。複雑なニューラルネットワークの学習も、原理的には全く同じです。
まとめ
- Tensor はデータ構造+自動微分を担う重要な要素。
requires_grad=Trueで自動微分の対象を明示。backward()で勾配計算、optimizer.step()でパラメータ更新。optimizer.zero_grad()を忘れずにリセット。
コメント