【理論基礎５】ニューラルネットワークの層構造とその役割

ニューラルネットワークの基本構造

ニューラルネットワークの各レイヤーは、大きく3つのカテゴリーに分けられます（ページの真ん中、「全体の構造と表記」の図を参照）：

• 入力層（Input Layer）
• 隠れ層（Hidden Layer）
• 出力層（Output Layer）

入力層と出力層

入力層は、モデルがデータを受け取る部分です。このデータは数値化され、一般に入力層の値を \(x = (x_1, x_2, …, x_n)\) と書きます。この層の役割は、モデルに外部からの情報を入力することです。たとえば、画像認識モデルでは、画像の各ピクセル値が入力として使われます。

出力層は、モデルが計算の結果として予測を出す部分です。たとえば、手書きの数字の認識であれば、出力層が「0〜9の数字のいずれか」という答えを提供します。この層の出力は図の例であれば、手書き文字が各数字である確率で、\(y = (y_1, y_2, …, y_k)\) のように書かれます。ここで、k はクラスの数です。

高校数学で関数を \(y = f(x)\) と表したのと同様に、ニューラルネットワークも入力 \(x\) を受け取り、出力 \(y\) を返す高度な関数として捉えられます。

隠れ層

隠れ層は、入力層と出力層の間に位置し、複雑な計算を担う部分です。隠れ層の各ニューロンでは、入力値の重み付き総和とバイアスが計算され、その結果が活性化関数を通じて次のレイヤーに送られます。

各レイヤー \(l\) の隠れ層の出力をベクトルとして \({\boldsymbol z}^{(l)} = (z_1^{(l)}, z_2^{(l)}, …, z_m^{(l)})\) と表します。たとえば、1つ目の隠れ層の出力（ベクトル）は \({\boldsymbol z}^{(1)}\)、2つ目の隠れ層の出力は \({\boldsymbol z}^{(2)}\) です。

これまでの説明で、最初のレイヤーが \(x\)、次のレイヤーが \(z^{(1)}\) という表記になっていた理由は、入力層と中間層、レイヤーの概念を意識していたためです。

全体の構造と表記

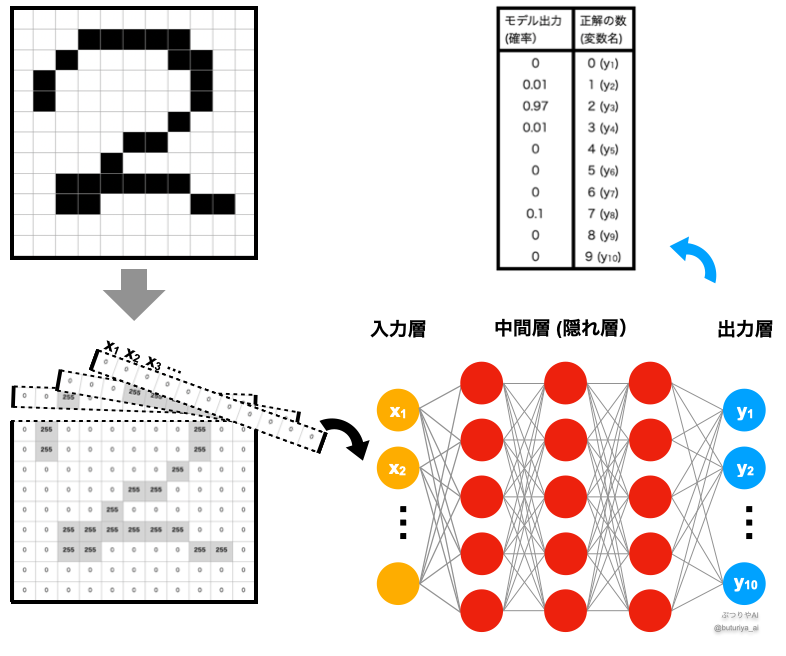
ニューラルネットワーク全体の簡略化と応用例として、以下の図のように表現できます。図右下を見ると、入力層、隠れ層、出力層が連なり、各層の出力が次の層の入力として扱われます。

さらに、活性化関数や重み行列を用いると、層間の関係は以下のように数式で表されます:

$${\boldsymbol z}^{(l)} = \varphi \left({\boldsymbol W}^{(l-1)} \cdot {\boldsymbol z}^{(l-1)} + {\boldsymbol b^{(l-1)}}\right)$$

ここで、

• \({\boldsymbol W^{(l-1)}}\): \(l-1\) 層と \(l\) 層を結ぶ重み行列
• \({\boldsymbol b^{(l-1)}}\): \(l\) 層のバイアスベクトル
• \(\varphi\): 活性化関数

です。

図の中では、入力は手書き数字の各ピクセルの値です。ピクセルは全部で \(11\times11=121\) 個なので、入力層は \((x_1, x_2, …, x_{121})\) となります。出力層は、入力された画像にかかれている数字が0~9のいずれかである確率になるので、\((y_1, y_2, …, y_{10})\) となります。

まとめ

ニューラルネットワークは、入力層、隠れ層、出力層という3つの基本的なレイヤーで構成されます。それぞれが異なる役割を持ち、特に隠れ層が複雑な計算を担う重要な部分です。各レイヤー間の関係を数式や図で整理することで、全体の構造を直感的に理解しやすくなります。

次の記事では、入力が画像の場合、この構造を基にディープラーニングがどのように学習を行うのか、その仕組みについて掘り下げていきます。